文|章仕仁

編輯|章仕仁

在追求高精度的現代數控系統中，熱誤差即熱變形誤差越來越受到人們的重視，根據研究表明，熱變形誤差已經是數控機床最主要的誤差來源，達到總誤差的40%~70%。

由于機床內部熱源較多，在傳熱和散熱時彼此又相互影響，再加上其他因素，使得對熱誤差的建模變得很困難，為了盡量減少這些誤差對加工精度的影響，大量的基于誤差補償的方法得到了充分研究和發展。

這些方法的基本假設是：機床誤差是由溫度分布，位置以及軸運動方向確定的函數。

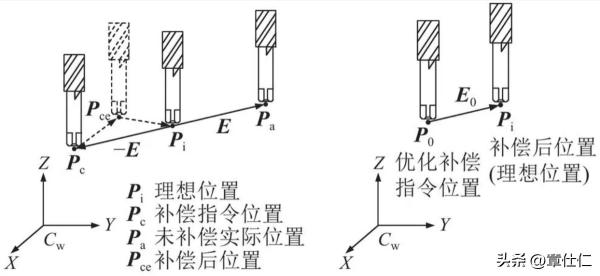
在獲得這些信息后，就可以構建一個溫度與其相應的誤差的模型，然后通過這個模型誤差項可以被預測，進而將其實時補償到加工過程中，從而提高工件加工的精度。

目前，國內外在對熱誤差進行建模過程中比較常用的建模方法，是利用數據擬合的方法來構建離散溫度點和熱誤差之間的經驗關系，其中基于神經網絡的建模方法得到了廣泛的研究。

這些方法大多對機床的主軸進行了熱誤差建模，在研究中著重討論其在機床的直線進給系統滾珠絲杠熱誤差建模中的應用，根據訓練數據集的特征引進了一種數據預處理的方法，最后實驗結果表明，神經網絡系統在熱誤差建模精度上將最大誤差由10pm 降低到2um。

絲杠熱誤差分析

滾珠絲杠由螺桿、螺母和滾珠組成，它是工具機和精密機械上最常使用的傳動元件，其主要功能是將旋轉運動轉換成線性運動，或將扭矩轉換成軸向反覆作用力，同時兼具高精度、可道性和高效率的特點。

機床直線進給系統中的滾珠絲杠在高速條件下運行時，滾珠絲杠受運行時間和運行速度影響而溫度上升，導致滾珠絲杠產生熱變形，使得加工精度下降。

除了摩擦熱以外，環境溫度變化對絲杠的熱變形也有一定的影響。

人工神經網絡

人工神經網絡是一種計算模型，由大量的節點相互連接而構成，更重要的是人工神經網絡它能夠通過運用已知實驗的數據來學習和歸納總結，然后將學習的結果泛化到一般情況。

實際中常用的是三層神經網絡，它包含輸入層隱藏層和輸出層，在輸入層各個神經元接收大量非線形輸入信息，輸入信息在神經元鏈接中傳輸、分析、計算，最后形成輸出結果，在輸出層中輸出。

隱藏層是輸入層和輸出層之間眾多神經元和鏈接組成的各個層面，隱層的神經元數目不定，但數目越多神經網絡的非線性越顯著，從而使神經網絡的強健性更顯著，如圖1所示為一個典型的三層前饋神經網絡。

在圖1中，該網絡輸入層神經元個數為4個，輸出層神經元個數為1個，隱藏層的神經元數量為9個。

通過訓練樣本的校正，對各個層的權重進行校正而建立模型的過程，我們稱之為學習過程，具體的學習方法則因網絡結構和模型不同而不同，常用的是反向傳播算法(BP算法)。

BP算法可以用來訓練多層網絡，它采用使均方誤差最小化的最速下降法，基本的BP算法的一個主要缺陷是訓練時間較長，使用基本BP算法解決實際問題不可行。

我們主要采用改進的BP算法——Levenberg-Marquard BP算法(LMBP)來提高算法的性能。

LMBP算法是在最速下降法和高斯牛頓法之間進行平滑調和，當在遠離最小值時逐漸切換到高斯牛頓法，所以它既有高斯牛頓法的局部收斂性，又具有最速下降法的全局特性。

由于 LMBP 算法利用了近似的二階導數信息，因而它比最速下降法快得多，由于 LMBP 算法是采用更加有效的數值計算優化方法來改進基本 BP 算法，從收斂速度和收斂性角度看，它是最速下降法和牛頓方法的折中，從而實現了收斂速度和穩定性的統一。

絲杠熱誤差建模

在本節中，將通過實現一個實際的神經網絡模型，來詳細地考察它在對滾珠絲杠熱誤差建模應用上的具體情況。

在建立 ANN 模型時有幾個步驟需要考慮，第一，選擇什么樣的網絡結構，選擇三層前向網絡結構，典型的如圖 1所示的三層前向神經網絡結構，輸入層和隱層的神經元傳輸函數為 S型函數輸人層傳輸函數為線性函數。

第二，選擇學習方式，我們選擇使用有監督的學習方式，即網絡訓練是基于定數量的訓練樣本進行的。

第三，選擇學習算法，我們選擇對基本 BP 算法進行改進的 LMBP 算法，所建神經網絡模型的輸入為一個四元組(環境溫度，滾珠絲母溫度，前軸承溫度，位置)，輸出為絲杠熱變形量，即要預測的熱誤差值。

訓練數據集的構成形式為：E其中 E =(TPQ)，T=(T，T，T)表示溫度輸入量，它們分別是環境溫度，滾珠絲母溫度和前軸承溫度。

P表示某一個位置，Q為對應熱變形量，E表示數據集中一個元素，含義是在 T溫度條件下位置 P處的熱變形量。

事實上，整體數據集可視為一個溫度一位置一熱變形量的三維矩陣，每一個數據元素都包含溫度、位置和相應熱變形量。

訓練數據的一個重要特征是存在大量的重復性數據，從而不能將它們直接用于模型訓練，例如在某一溫度條件下，絲杠不同位置處都要檢測熱變形量，這時溫度值存在大量重復，因而這些數據需要經過預處理才能應用于模型的訓練。

預處理方案的核心思想是選擇不同溫度，不同位置的數據構成一次訓練的數據子集，然后用這些不同的子集重組成最終的訓練數據集。

在實驗中，采取了循環取矩陣對角線位置的方法來達到溫度不同、位置不同的效果。

在預處理數據過程中為操作的復雜度，將溫度數據和位置一熱變形量數據分開保存在兩個矩陣里，這樣可以得到兩個二維數據矩陣：位置-熱變形量矩陣(P)和溫度矩陣(C)，這時問題簡化為從 P 矩陣中選擇有限個不同行不同列的數據元素，簡單有效的方案是沿著對角線的方向取不同的元素，并將之與溫度矩陣 C中的元素拼湊成一個訓練數據子集。

循環從位置一熱變形量矩陣取對角線元素可以保證充分使用原始數據，數據預處理流程圖如下圖 2 示。

該數據預處理方法具有簡單靈活的特點，它很容易通過編程進行實現，而且可以避免在三維空間中進行復雜的選取操作。

經過預處理后的訓練數據由不同的溫度條件和不同的位置及其對應的實際熱變形量組成，從而可以使模型進行了充分的學習，從而可以增強模型泛化的能力。

本實驗以VMCO850B 三軸立式加工中心的Y軸直線進給系統的熱變形誤差為研究對象，Y軸進給系統：Y軸最大行程為380mm，在機床冷態下定位誤差+1um，使用 TSic306 數字式溫度傳感器，測量范圍-50C至+80C，測量精度0.3C，分辨率0.1℃，使用ML10 激光干涉儀檢測Y軸定位誤差。

實驗環境如下圖 3 所示。

實驗流程

實驗主要分為兩個階段，第一階段是數據預處理和神經網絡的模型訓練，第二階段是模型泛化，即利用訓練好的模型來預測特定加工條件下的熱誤差，通過與實際測量的誤差對比來檢驗模型的精度。

實驗流程如下圖4 所示。

在建模實驗過程中，隱層節點數的選擇是一個很復雜的問題，隱層節點數過少，容錯性差，識別未經學習的樣本能力低，相反，如果過多則會增加網絡的訓練時間，同時還可能樣本中非規律性的內容存儲進去，從而降低了泛化能力。

下面為一個確定隱層節點數的經驗公式：l=/n+m +a

其中，l為隱層節點數，m 為輸入節點數，n 為輸出節點數，a為1~10之間的調節常數，在實驗中為了簡化該問題，先根據經驗公式假設隱層節點數為5，然后根據訓練結果的均方誤差不斷調整參數a，最終確定隱層節點數為9可以達到預期的期望，即使得均方誤差最小。

數據檢測系統將采集所有用于模型訓練的數據，主要包括：D溫度采集，為了獲得滾珠絲杠平均溫度，分別在絲杠發熱最大的前軸承和滾珠絲母處各安裝一個溫度傳感器，如下圖 5 所示，另外安裝一個檢測環境溫度的變化，@熱變形量檢測，利用ML10激光干涉儀檢測Y軸絲杠在不同溫升時、不同位置處的熱變形。

通過對采集的數據進行初步統計，環境溫度數值變化范圍是 6.9 ~9.5，滾珠絲母溫度數值變化范圍是 3.8~11.8，前軸承溫度數值變化范圍是 6.220，最大熱變形量的變化范圍0~-73um(負號表示負半軸方向)，可以看出環境溫度變化比較小，而前軸承溫度變化最大。

模型訓練及其結果

在對訓練數據進行預處理后，使用 LMBP算法對神經網絡模型進行訓練，一般情況下對模型的訓練需要經過多次的訓練才能達到理想的效果，這主要取決于模型參數的初始化情況。

圖6所示為在溫度(7.8，9.5，19.6)條件下的訓練結果，其中溫度值分別為環境溫度、滾珠絲母溫度和前軸承溫度，從圖中可以看出，訓練后的模型的輸出值能很好逼近測量的真實值。

通過對建立的神經網絡進行訓練，最終成功地實現了對數控機床直線進給系統的熱誤差進行預測。

圖7顯示了在實際采集的溫度(7.8，9.15，19.1)條件下，神經網絡模型和最小二乘法擬合法對 Y軸的熱誤差的預測值和實際誤差值，其中溫度值分別為環境溫度、滾珠絲母溫度和前軸承溫度。

另外，最小二乘法模型為本課題的現有成果，圖8 顯示了在Y軸190mm處兩種模型輸出的結果對比效果，為了作圖方便橫坐標只選擇前軸承處溫度值代表相應的溫度環境，圖7給出了位置-熱變形量的二維結果圖，圖8給出了溫度-熱變形量的二維結果圖，通過對比兩個圖中的結果可以看出，神經網絡模型更好地實現了對絲杠熱誤差的預測，將最大預測誤差從10um降低到2um。

結語

我們主要闡述了將神經網絡用于滾珠絲杠熱誤差建模的過程，并根據原始數據的特點對其進行了數據重組式的預處理操作，然后使用預處理的數據進行了模型訓練。

實驗結果表明，神經網絡系統能夠很好的滿足預測精度要求，將最大預測誤差降低到2um。

以上兩個計算示例中，所給出的變密度法的優化結果均為去網格化以后的拓撲優化結果，從以上可以看出，若我們所采用的 KNN 方法得到的優化結果去網格化以后，與變密度法得到的優化結果很相似。

這說明我們采用的KNN方法是可行的，從單元保留或刪除的角度來考慮，可以將結構的拓撲優化設計歸結為一種結構單元的模式識別方式。

KNN算法廣泛地應用于各種模式識別中，我們是在建立了連續體結構數學模型的基礎上，將 KNN算法引入到結構拓撲優化設計領域中，給出了單元識別的歐氏距離判據公式以及識別標準，并對幾個經典的算例進行了計算，所得優化計算結果與其他連續體拓撲優化設計方法得到的結果很相似。

這表明優化結果是正確的，同時也說明 KNN方法在結構拓撲優化設計領域的應用是可行的，這為連續體的結構拓撲優化設計提供了一種新方法，并拓展了KNN算法的應用領域。

轉載自頭條號：章仕仁。（侵刪）